Voronoi

I decided to swap my IDE from the default Processing IDE to IntelliJ IDEA. While the Processing IDE worked fine for the most part, what I like about IntelliJ is:

• The ability to have only specific files open

• Compressing/hiding irrelevant functions

• Better code completion

While none of these features were necessary, I started to feel like I had too many files to manage in processing, and I would sometimes get lost trying to find a function.

As for some of my work this week, I started out by experimenting what to do with the leaves on my trees. By deleting them entirely, I found that each tree seemed more visually discrete.

I also experimented with simply cutting the radius of all leaves in half, but it didn’t look very nice.

A compromise between the two is to cut the radius in half (or by any amount) and then to move the circle to be touching its parent.

While I still haven’t decided which approach I like best, I do have more ideas for making the trees more visually discrete, including deleting entire trees as necessary.

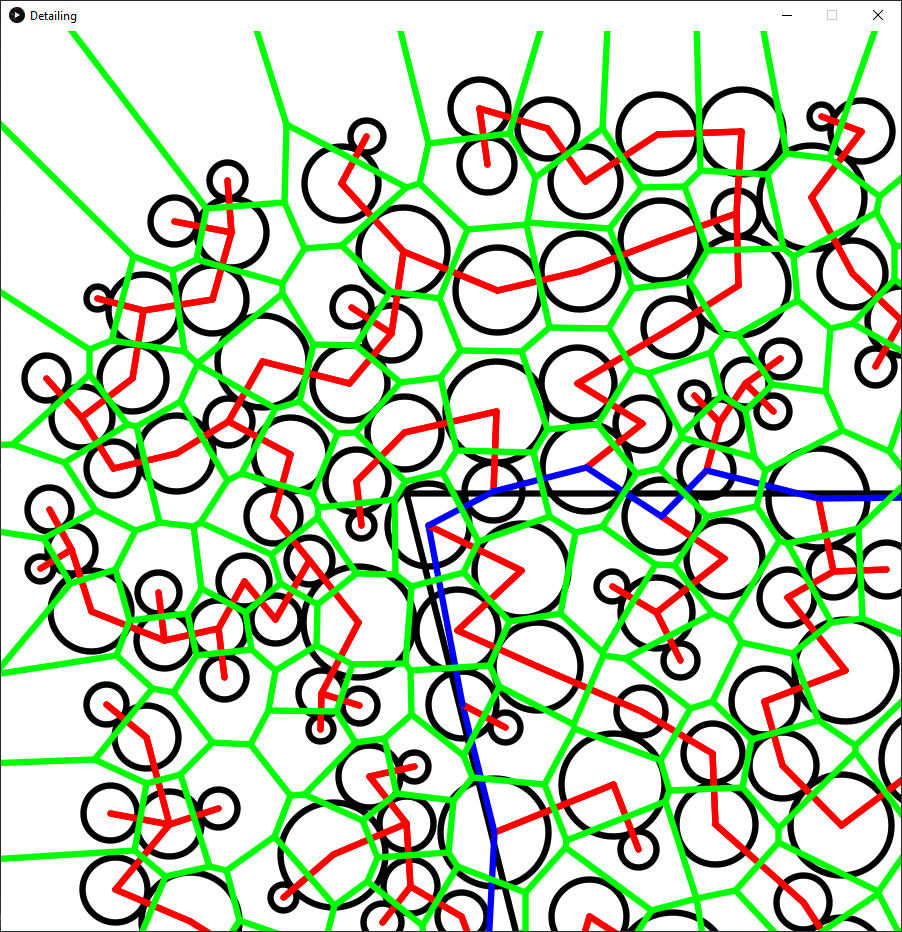
I decided to swap the library I used to get my Delaunay Triangulation. I found the new library was slightly faster, but the main benefit was that it also provided a method of getting the Voronoi diagram. While this diagram is not fully accurate as it interprets each circle as a point, disregarding its radius, I have been experimenting to see if it had any use.

One simple idea is to use the diagram to increase the density of the circle packing. Any point in the diagram where three lines meet is in theory equidistant from each point. However, as I mentioned the diagram did not take into account the radius of the circles so this was not generally the case. While it is possible to generate a tiling such that the radius of each circle is represented, I didn’t see a library for it, and I ultimately found the uses of it limited. In any case, below is a simple example of using the Voronoi diagram to increase the density of the circle packing.

I also considered using the edges of the diagram as the basic structure of a curve. around the nodes. Unfortunately this would be problematic as each edge is shared by two nodes, so the curve would likely overlap itself frequently, even if a suitable path could be found.

Finally, as an example I have cherry-picked an example of my arc method of smoothing curves working around a random circle packing. While ideally I would want to have less of the shapes of the original circles visible, this does generally represent one of the ideas I am trying to accomplish.