Traversal 2

Continuing on from yesterday, I spent more time today trying to come up with a better way to traverse the trees I had created. The problem comes from the fact that I want to visit as many trees as possible, but the more trees I visit the more likely I am to have a line connecting two trees passing straight through a third. While ensuring that no lines cross is still a while away, I want to avoid it as much as possible.

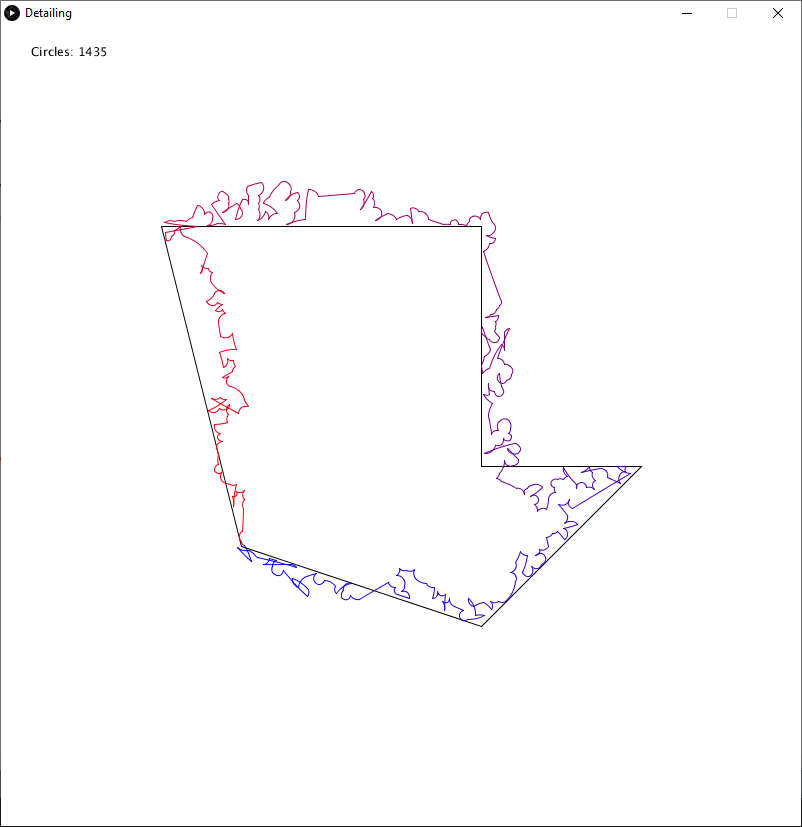
I started off by implementing a method I mentioned previously, where instead of having one node that the traversal of each tree would begin and end on, I would have a start node and an end node. While I believe this helped reduce instances of connecting lines cutting across trees, its limitation is that it will ignore many nodes as seen below.

Note - this image was generated using a denser circle packing than the others

The second method I tried was to create a minimum spanning tree of the minimum spanning trees, and select trees in order by traversing that. Unfortunately, this didn’t look much better.

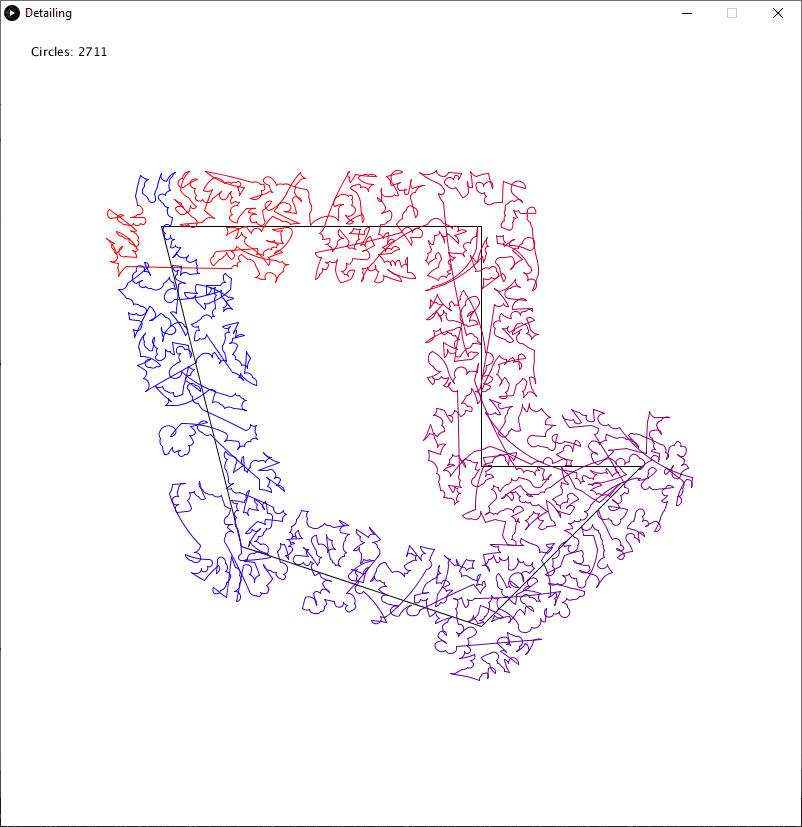
The final method I tried today was to reuse some code from earlier that traversed the Delaunay Triangulation. To do this, I chose a random node from each minimum spanning tree, triangulated them, and then applied the algorithm I had previously written (I had hoped it would come in handy). Unfortunately, this method proved to be too far on the other end of the spectrum, simply skipping most of the nodes (although it did not frequently cross over itself).

Tomorrow, I will keep searching for an ideal method.