Arcs 2

Over the past few days I’ve been attempting to create code to smooth a line around the perimeter of the circles on my trees by creating a new circle that touches two adjacent circles.

I have had some success. The code will in general do what I ask of it, but there are still many bugs to fix. Here is an example of the smoothing working properly:

The generated circles can have any radius, although by default I use half the average radius of the circles that I am connecting.

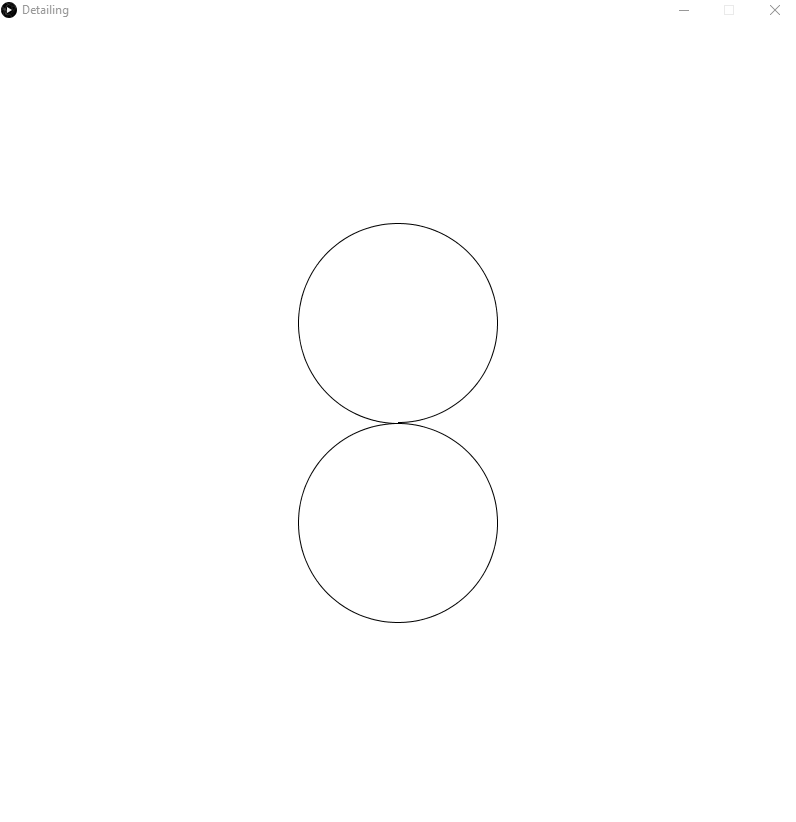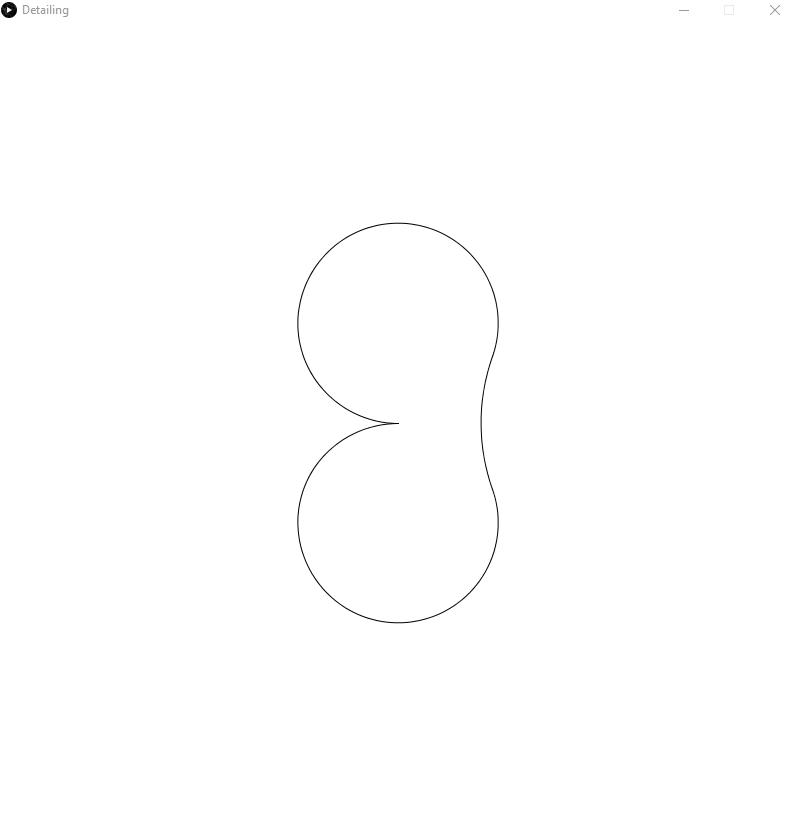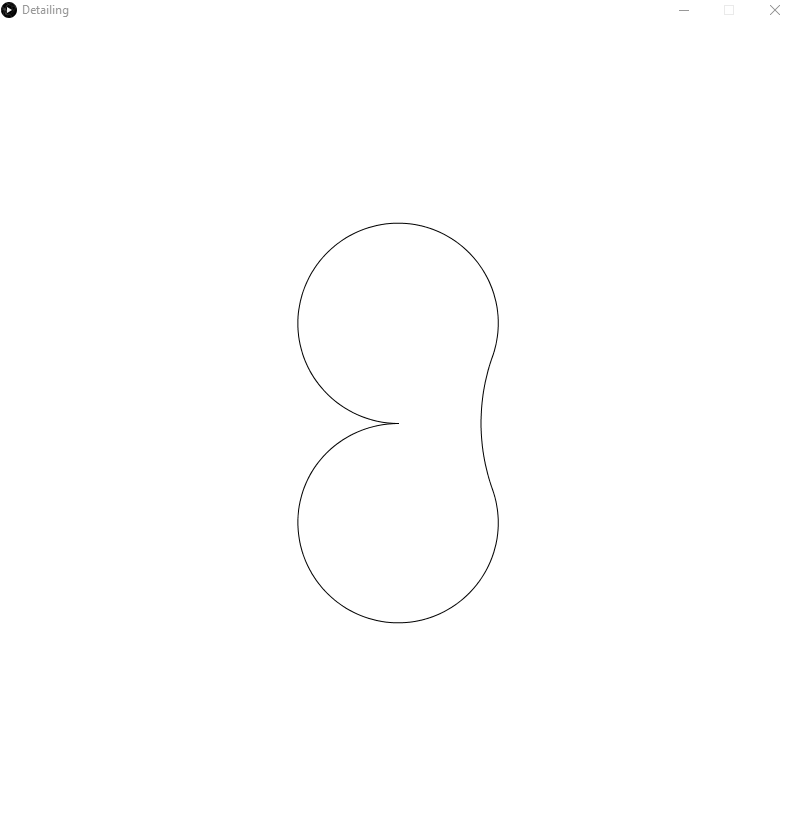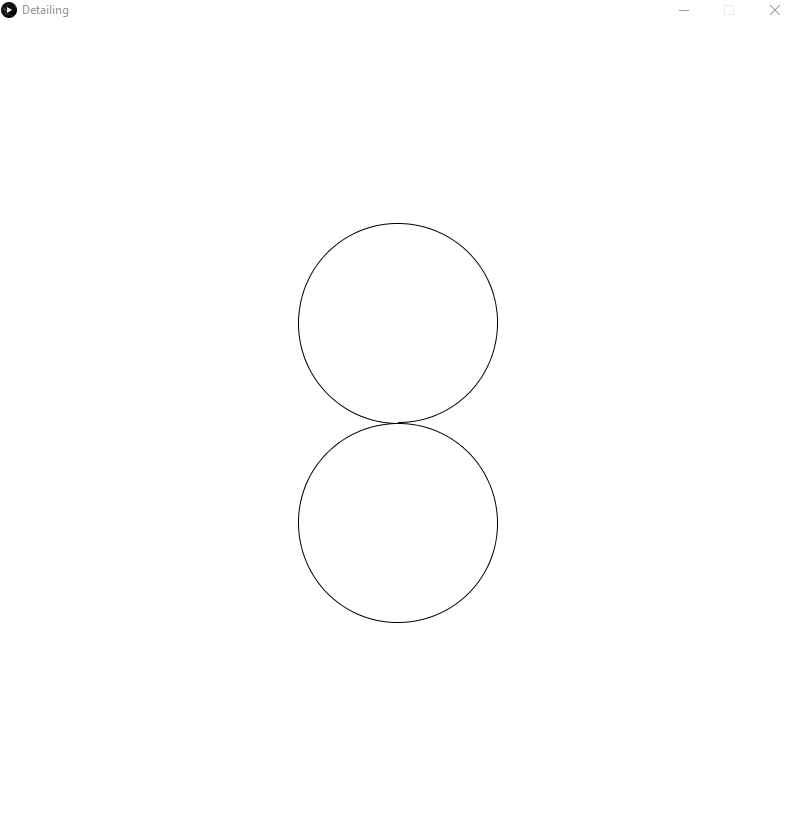
The circles that it is connecting also do not have to be touching.

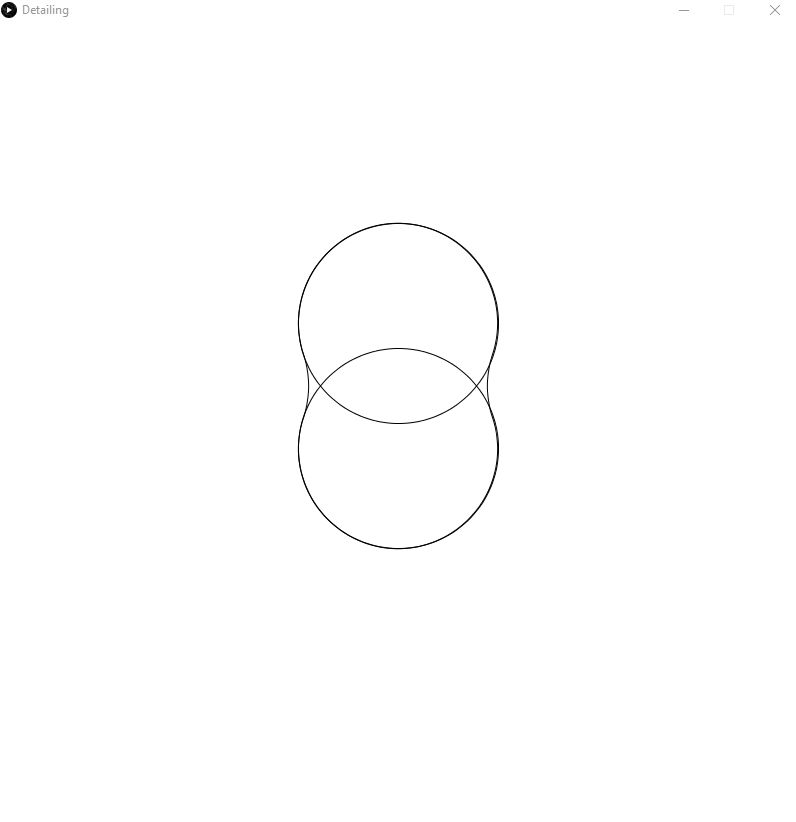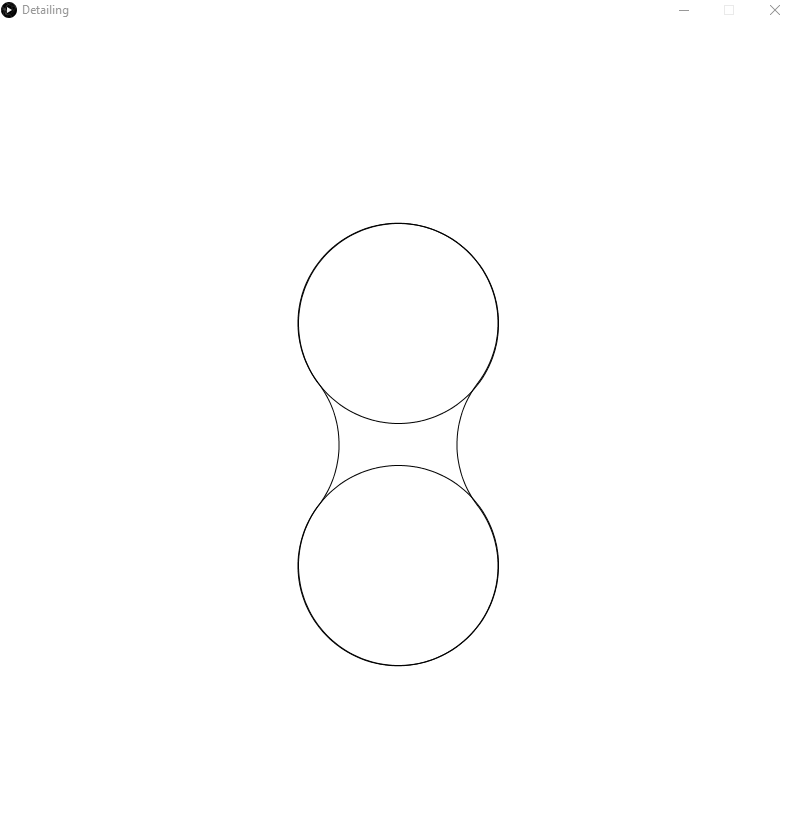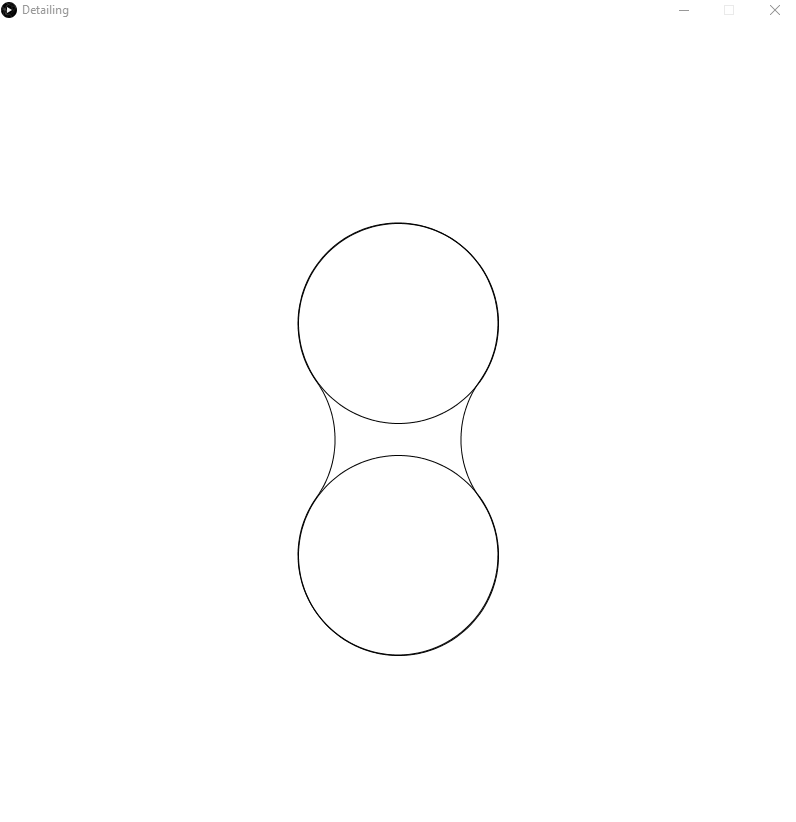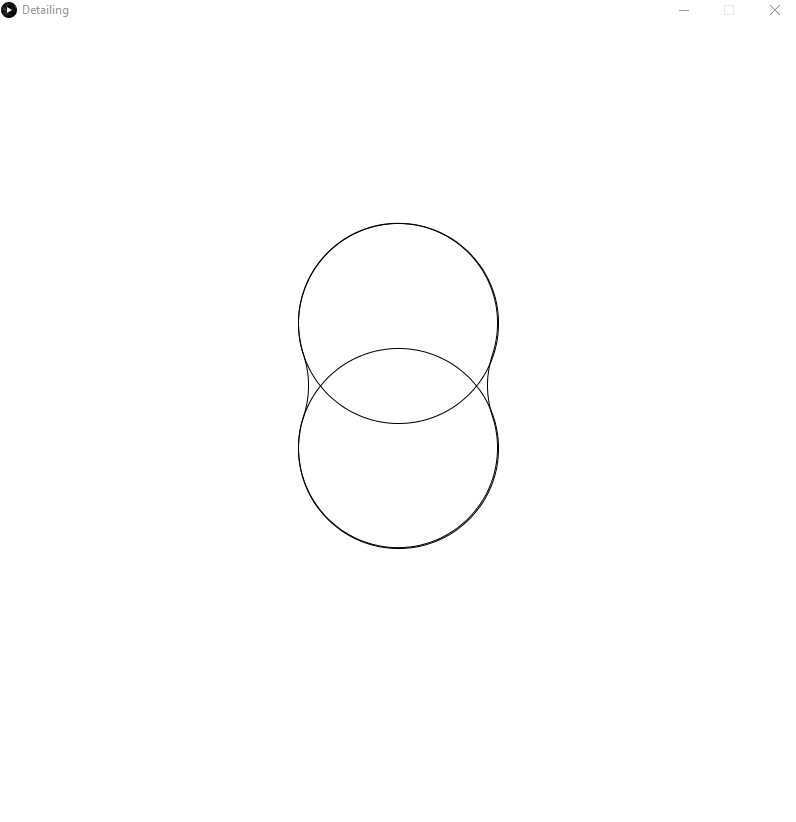
However, my initial method was slightly flawed. If one arc ended before another began, it would wrap all the way around the circle, as shown below:

I solved this by implementing another method of smoothing circles. Rather than calculate the arc from A to B, and then the arc from B to C, I calculated the arc that touched A, B, and C. This fixed some issues that I was having.

Notice how in the above animation the curve connecting the moving circle and the circle above it smoothly transitions to connecting three circles when it needs to.

Applying this to the traversal around the generated polyline, we get the following result:

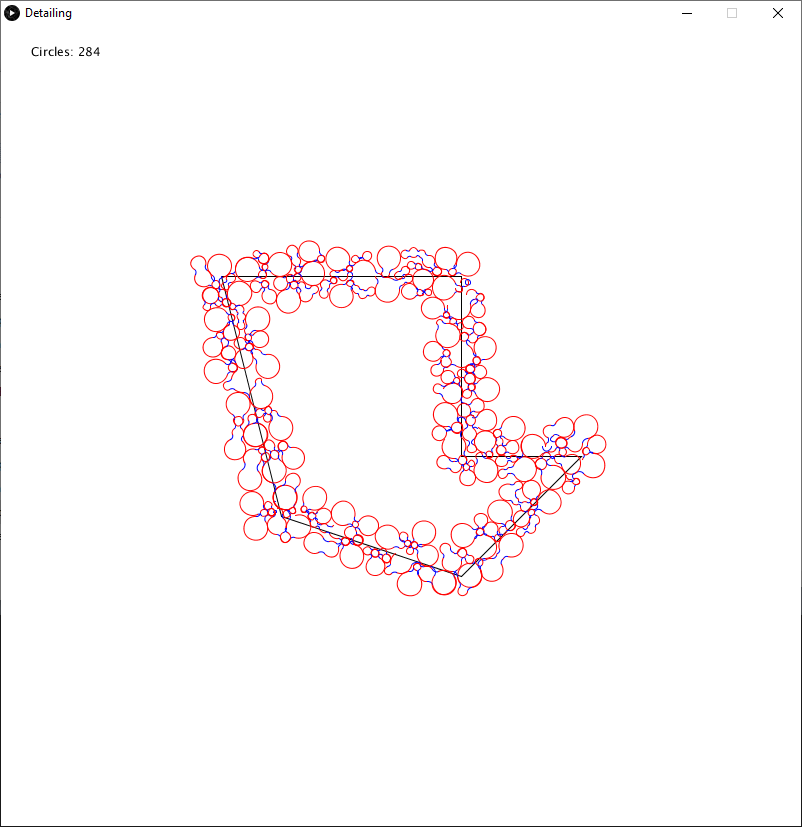
In this image, the blue lines represent the generated smoothing arc.

It is clear that my code still has many errors in it, but I believe that it shows a lot of promise. Of course, I still have some other issues to fix (such as swapping between trees and choosing stop and start nodes).

Here is a comparison between the generated curve and the original circle packing and traversal.

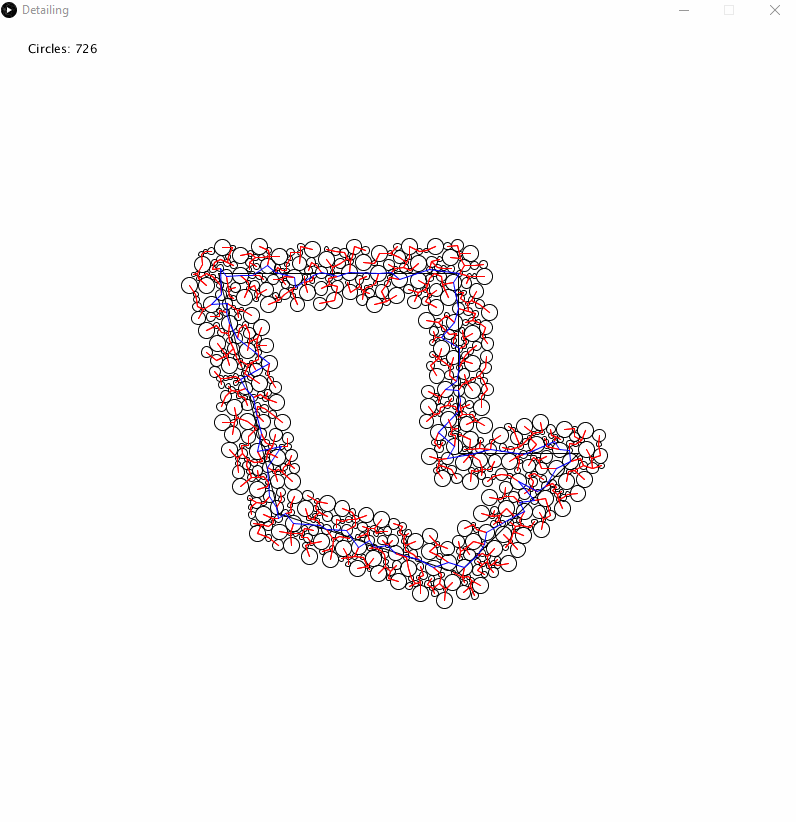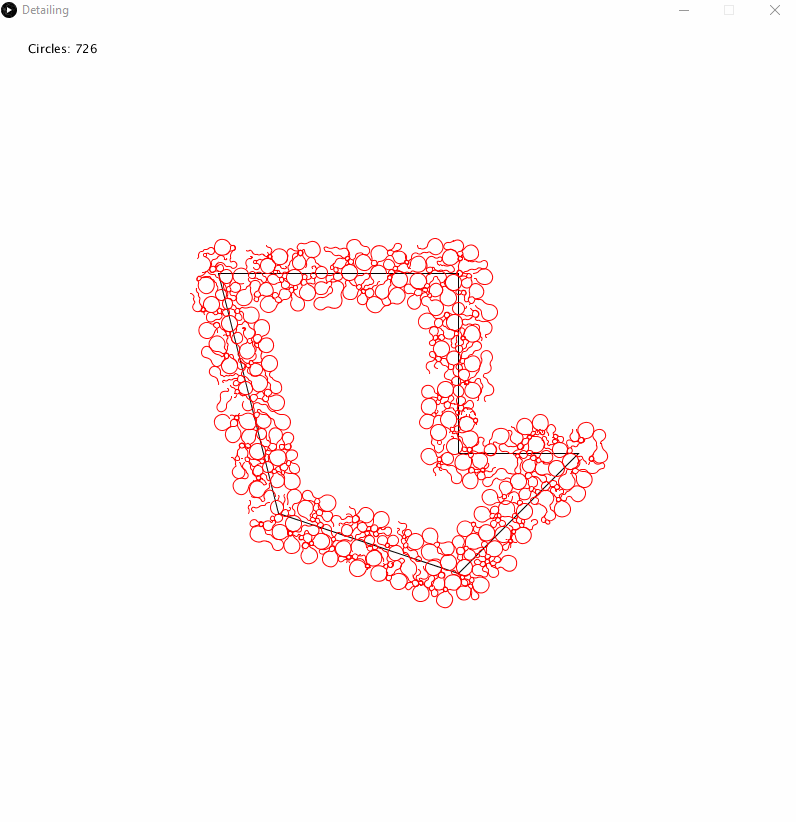
I’d like to make clear that I have not implemented clothoids, as I have not yet found a suitable library that makes it easy for me to generate them. This method merely swaps between arcs on circles.

Generating a circle that has the required properties (radius r, adjacent to circles x, y (, z)) is quite simple, only requiring some basic algebra that can be easily written as code. However, there are two areas of difficulty after that.

Firstly, the correct circle must be selected. There are two circles that touch any three circles, and there are two circles that touch any two circles with the required radius. While this is trivial for a human to decide, it was harder to put into code, although I believe that I have successfully completed this portion.

Secondly, the suitable arc on the perimeter of the circle must be found. Again, while this is trivial for a human it is harder for a computer. The start and stop angles must be provided in the correct order in the correct period, and they can be difficult to calculate properly as I dynamically swap in between my methods of smoothing the circles.