Kruskal

As an experiment, I wrote an algorithm that uses the Delaunay triangulation to move around the shape. It simply selects a start point, then moves to whichever node it shares a corner with that has the minimum angle with the next vertex it’s trying to reach. There is also a check to ensure that it doesn’t double back on itself.

To simplify matters, after generating a triangulation of the vertices I added a requirement that no edge could be too large, which got rid of may unnecessary edges.

To add even more available circles, I added a variable which when increased worked to decrease the possible sizes of circles. This resulted in tighter, smaller packing.

However, for general testing I will leave the circles large as generating tighter packings require much more time.

I was also able to implement Kruskal’s algorithm to find a minimum spanning tree of the circles generated.

By adding a requirement that no two graphs may be connected if the size of the existing graph is greater than an integer N, I was easily able to split it up into smaller trees.

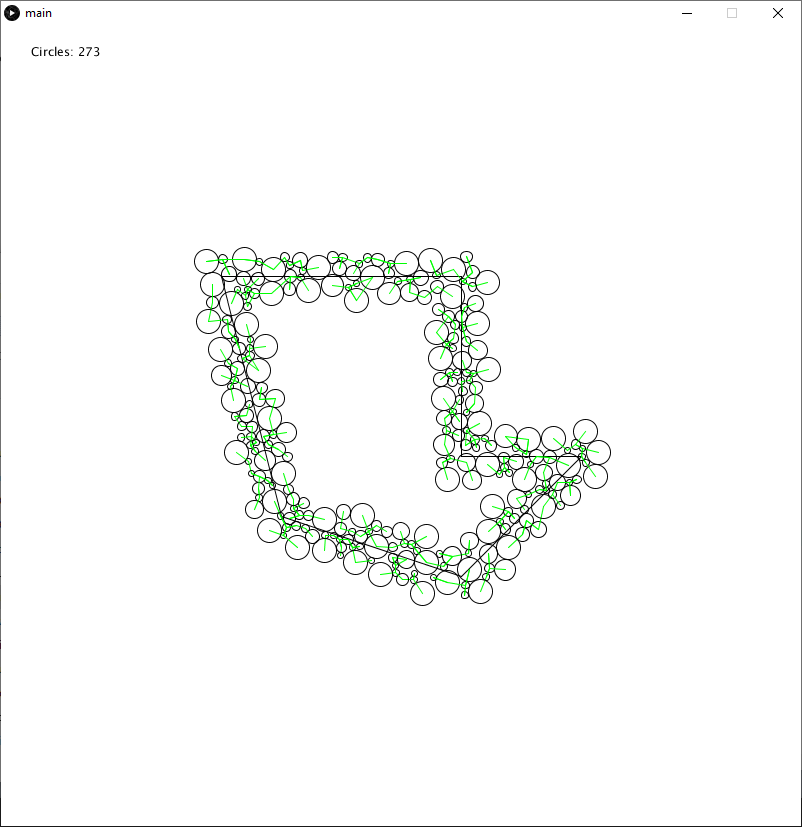
If you look closely, some of these graphs are not actually trees. It’s unclear why this is, but I have some theories I will investigate tomorrow.

As well, I have made good progress on an algorithm that can number these trees so that they may be selected in order to be traversed, but I was unable to finish it today.