Java

Today I mostly finished my move to Java and significantly improved my code. The combination of Java running faster and me being forced to rethink my code as I rewrote it has improved speed several dozen times over.

Moving to Java also allowed me to implement a library that calculates the Delaunay Triangulation of a set of points for me. In short, the Delaunay Triangulation of a set of points is the triangulation such that the circumcircle of each triangle contains no other points in the set.

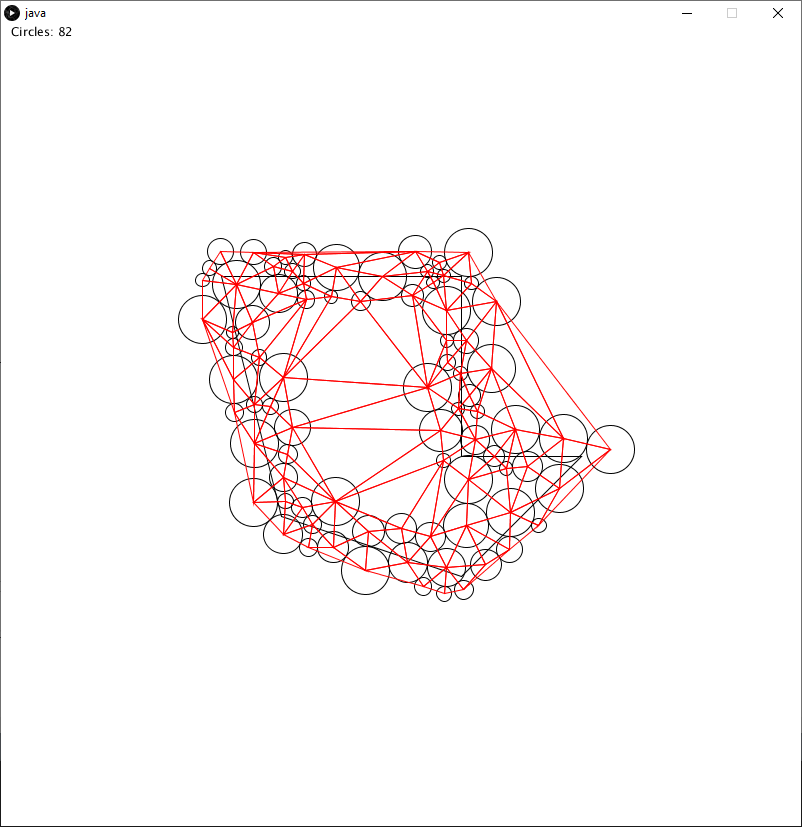
An example triangulation can be seen below.

Here, I’ve overlayed every circumcircle over the shape.

The Delaunay Triangulation can be easily applied to a circle packing of the shape.

The following image contains the circumcircle for each triangle and is quite messy, but it provides me with a lot of oppurtunity.

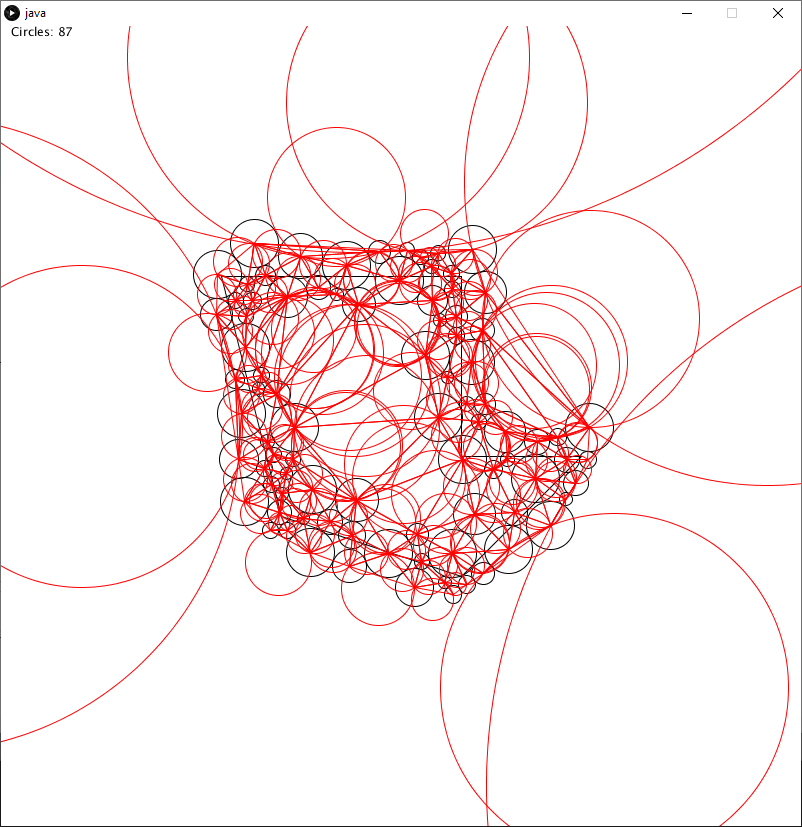
While this image is very busy, most of the circle will remain unused in a final version of this method. What I can now do is navigate around the shape (using the triangulation, the touching circles, or some other method), and between each node I can simply draw an arc following the circumcircle.

I’ve drawn a rough sketch of what that could look like below.

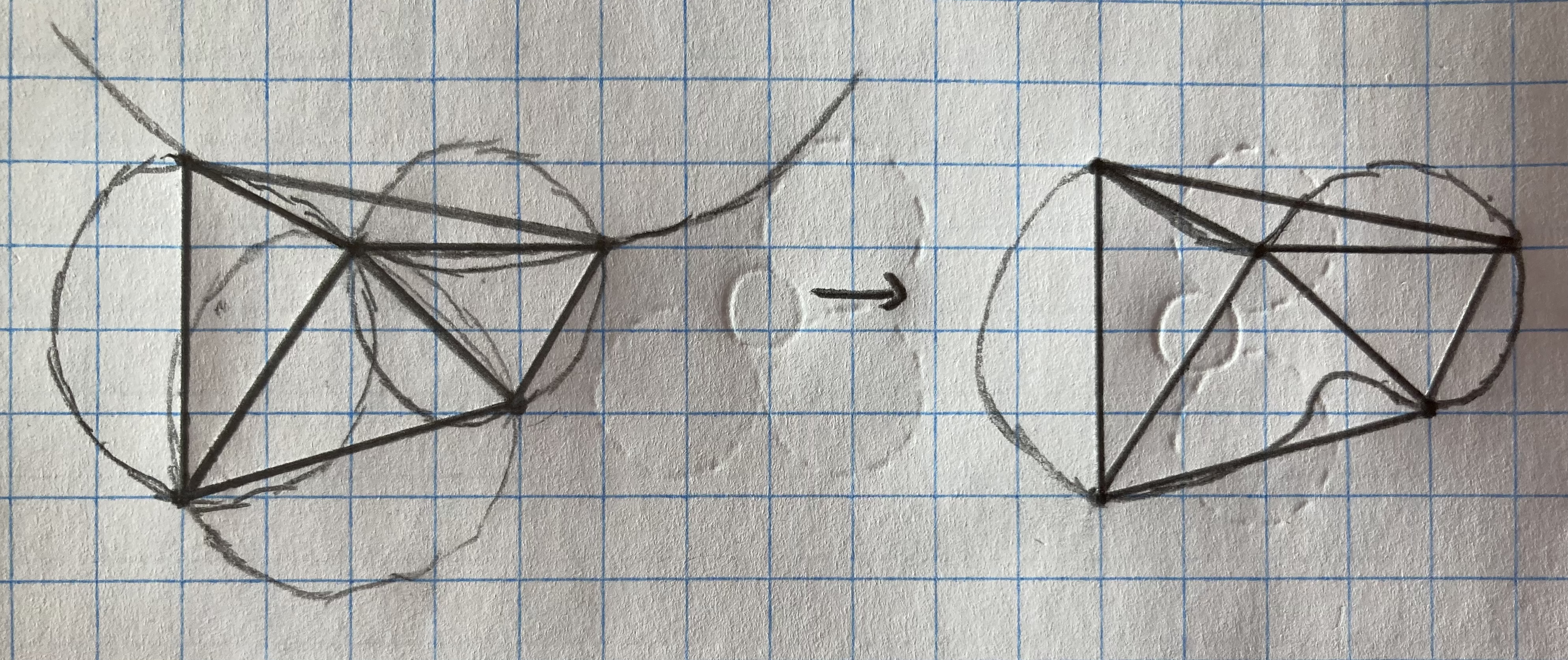
In reality, the vastly increased number of circles would result in a curve that more closely followed the polyline, not just individual circles.